| |
|
|
|
| |
|
|
 |
 ESTRUCTURAS
- Sistemas de fuerzas concurrentes: resolución gráfica y analítica ESTRUCTURAS
- Sistemas de fuerzas concurrentes: resolución gráfica y analítica |
|
|
| Un sistema de fuerzas concurrentes es aquel
para el cual existe un punto en común para todas
las rectas de acción de las fuerzas componentes.
La resultante es el elemento más simple
al cual puede reducirse un sistema de fuerzas. Como simplificación
diremos que es una fuerza que reemplaza a un sistema
de fuerzas. Se trata de un problema de equivalencia
por composición, ya que los dos sistemas (las
fuerzas componentes por un lado, y la fuerza resultante,
por el otro) producen el mismo efecto sobre un cuerpo.
En el ejemplo que veremos a continuación vamos
a hallar la resultante en forma gráfica y en forma
analítica. |
| |
 EL
SISTEMA EL
SISTEMA
-
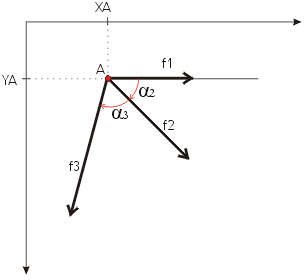
Las fuerzas componentes son f1, f2 y f3.
- El punto en común por el que pasan las rectas de acción
de las fuerzas componentes es A, cuyas coordenadas son (XA,YA).
- Para definir la resultante R deberemos obtener su módulo, dirección
y sentido (argumento) y las coordenadas de un punto cualquiera de su
recta de acción...
...como
veremos a continuación, su módulo se
obtiene midiendo con una regla en el gráfico
y multiplicando por escala de fuerzas (por ejemplo:
tn/cm).
...y su argumento se obtiene midiendo con transportador el ángulo
que va desde el eje X hasta la fuerza, barriendo en el sentido de giro
adoptado (horario o antihorario).
...y las coordenadas de un punto cualquiera de su recta de acción ya
las conocemos, porque tratándose de un sistema de fuerzas concurrentes,
la recta de acción de la resultante R también pasará por
ese punto A.
|
| |
RESOLUCIÓN GRÁFICA
Ahora vamos a hallar la resultante en forma gráfica. Para ello, considerando
los datos dados, definiremos una escala de fuerzas (tantas toneladas equivalen
a tantos centímetros dibujados en la hoja de papel). Luego iremos
armando el polígono de fuerzas, dibujando una a una las fuerzas,
una a continuación de la otra, respetando la longitud y el ángulo
de cada una de ellas.
Datos del sistema:
f1=3t - 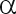 1=0º /
f2=4t - 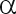 2=45º /
f3=5t - 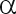 3=105º /
A=(3,2)
Esc. fzas. = 1tn/1cm
Giro en sentido horario
|
|
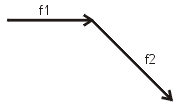
(1) Utilizaremos regla
para dibujar las fuerzas y transportador para
trazar los ángulos... Considerando los
datos, dibujamos la f1. En nuestro caso medirá 3cm.
|
|
|
(2) A continuación
de f1, dibujamos la f2 que medirá 4cm.
|
|
|
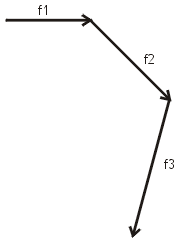
(3) A continuación
de f2, dibujamos la f3 que medirá 5cm.
|
|
|
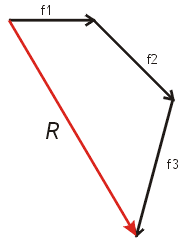
(4) Ahora dibujamos la fuerza resultante,
que surge de unir el comienzo de la f1 con
el extremo de la f3. La "flecha" de
la resultante va hacia la "flecha" de
f3, la última fuerza. ¿Y esto
por qué? Porque estamos hallando una
fuerza (la resultante) que es equivalente
a las tres fuerzas componentes de nuestro
sistema (f1, f2, f3).
|
|
|
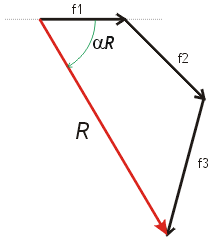
(5) Midiendo con la regla la longitud
de la resultante obtenemos su módulo.
Midiendo con transportador el ángulo 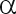 R
obtenemos su argumento. R
obtenemos su argumento.
Esto es: 8,8cm - 59º
|
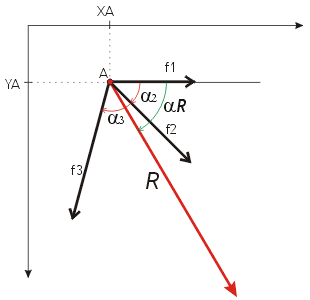 |
(6) Y para finalizar, transportamos
en forma paralela la recta de acción
de la resultante -usando la regla y la escuadra-
haciéndola pasar por el punto de aplicación
A. Ya hemos resuelto el problema en forma gráfica.
Siendo: R=8,8t - 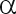 R=59º R=59º
|
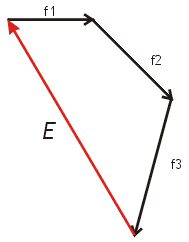 |
(7) La fuerza equilibrante surge
de unir el extremo de la f3 con el comienzo
de la f1. La "flecha" de la equilibrante
va hacia el comienzo de f1, la primera fuerza.
Conforman un polígono de fuerzas cerrado.
La equilibrante es una fuerza de igual recta
de acción, intensidad y sentido contrario
que el de la resultante. Se trata de un problema
de equilibrio por composición.
Siendo: E=8,8t - 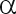 E=239º E=239º
|
|
| |
RESOLUCIÓN ANALÍTICA
Ahora vamos a hallar la resultante en forma analítica. Recordamos
los datos del sistema:
f1=3t - 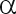 1=0º /
f2=4t - 1=0º /
f2=4t - 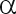 2=45º /
f3=5t - 2=45º /
f3=5t - 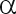 3=105º /
A=(3,2) 3=105º /
A=(3,2)
Primero vamos a hallar las proyecciones
de R: Rx y Ry
Luego, con Rx y Ry hallamos
la resultante R:
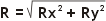
(esto nos dará el módulo)
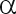 R
= arc tg Ry/Rx R
= arc tg Ry/Rx
(esto nos dará el argumento)
A=(3,2)
(es el punto de aplicación, dato del problema por ser
un sistema de fuerzas concurrentes)
|
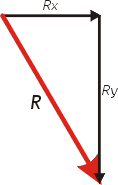
Esto lo escuché en las teóricas...
"Donde hay un triángulo, existe un triángulo de fuerzas" (contemporáneo
argentino)
|
Rx = 3t x cos 0º + 4t x cos 45º +
5t x cos 105º
Rx = 3t + 2,83t + (-1,29t)
Rx = 4,54t
Ry = 3t x sen 0º + 4t x sen 45º +
5t x sen 105º
Ry = 0t + 2,83t + 4,83t
Ry = 7,66t
R = 
R = 8,90t
Comparamos los resultados obtenidos
gráfica y analíticamente. |
|
| |
|
|
| |
 No
está permitida la copia, uso y/o reproducción de los artículos
sin autorización de sus autores. Está expresamente
prohibido reproducir parcial o totalmente cualquier
parte de este sitio sin autorización previa
y sin indicar la fuente. Para contactarse con Arquimaster realice click aquí. No
está permitida la copia, uso y/o reproducción de los artículos
sin autorización de sus autores. Está expresamente
prohibido reproducir parcial o totalmente cualquier
parte de este sitio sin autorización previa
y sin indicar la fuente. Para contactarse con Arquimaster realice click aquí. |
|
|
| |
|
|






 EL
SISTEMA
EL
SISTEMA